[머신러닝] 기초 개념 day3 (김용담 강사님)

강사님의 조언..

커리큘럼 따라가는거에 너무 목메이지 마라

개인마다 사정과 에너지가 다르고 파트별 이해도가 다르기 때문에

각자의 출발선이 다르기 때문에

모두가 만족할 수는 없다

강의는 참고용

어디를 모르는지 어디를 이해못했는지 찾고

복습하는게 중요하다

개인의 라이프사이클과 학습사이클을 최대한 지키면서

개인적인 페이스로 오래 가는게 중요하므로

이해 못했다 해도 좌절하지 말고

개인의 학습 효율성이 중요하므로

상태 안좋을 때는 너무 무리하지말고

긴 흐름

10개월 뒤에 무엇을 할 것인가

너무 이 과정에 매몰되지 않았으면..

다음주 머신러닝부터 체감 난이도가 확 올라감

첫번째 대규모 탈주가 시작된다

내가 이걸 이해 못하면 아무것도 못할거라는 생각을 하지만

100퍼센트 이해하고 코딩하는 사람은 거의 없음 현업에도

논문을 썼거나 연구를 했던 사람이 아니고는 100퍼센트 이해하기 힘들다

애초에 전부 이해하는게 힘들기때문에

모르겠는 내용을 체크한 뒤

나중에 찾아보면서 팔로업 하는게 좋음

머신러닝 엔지니어 과정이기 때문에 이론을 몰라도

충분히 프로젝트를 수행할 수 있다

선택과 집중

내가 아는 수준에서

내가 할 수 있는 최대한을 한 다음

열심히 찾아보면 이해할 수 있는 자료가 있다

그렇게 컨셉, 디테일 하나하나 쌓아야 한다

강의 피드백을 통해 강의의 난이도를 조절해라

---

“실제로 학습을 어떻게 하나요”라는 질문에 가장 확실한 답변

Loss Function을 통해 나의 머신러닝 모델이 어떻게 학습이 되는가

모든 모델이 오늘 설명하는것과 같이 학습을 하지는 않는다

지금 설명하는 모델의 가정은 parametic learning 자세히 말하면 (linear classifier, linear regression) 등이

이런 방식으로 학습을 한다

Loss Function

Loss Function의 목적

컴퓨터가 학습을 할 때 방향을 정해줘야함

P가 향상이 되려면 어떤 방향으로 학습해야 하는가

실제 정답 $y$와 $\hat y$의 차이가 적어지는 것

→ underline = Loss

Loss Function이 가장 작아지는 무언가를 찾고 싶음

우리가 이제까지 배워온 것은 $x$가 변수임

지금 여기서의 notation상으로는 $x$는 그냥 상수(주어지는 것)

$x$는 벡터가 될 수도 있고 숫자가 될 수도 있지만 지금은 그냥 숫자로 생각

이 때 우리가 바꿀 수 있는건 $w$와 $b$

우리는 $x$와 $y$를 알고 있음 (주어짐)

적당한 $w$와 $b$를 찾아주면 $y$를 알 수 있음

그런데 우리의 목표는 $y$가 아닌 $\hat y$임

#

Loss Function

학습의 목적은 무엇인가?

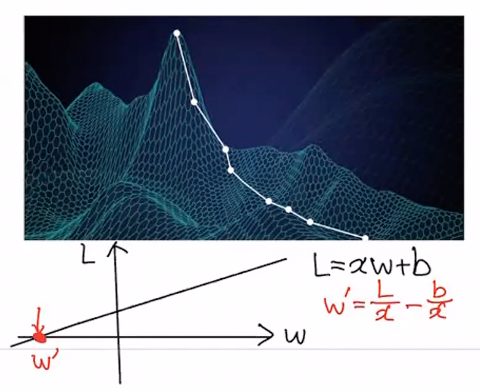
• Loss Function = Target Function
• Loss(error) = $y- \hat y$

Loss를 함수로써 정의하면 Optimization 할 수 있음

$y$ → target value

$\hat y$ → predicted value

• →차이

• Q1. Loss가 0이 되면 어떤 의미일까요?

• A1. $y = \hat y$

• Q2. Loss가 0이 되는 지점을 어떻게 찾을까요?
• A2. 정의한 loss function에서 L이 0이 되는 파라미터를 찾으면 됨. 여기서 파라미터는 $w$와 $b$ → 미분!

---

Loss Function Optimization

학습 목적의 최적 포인트를 찾자

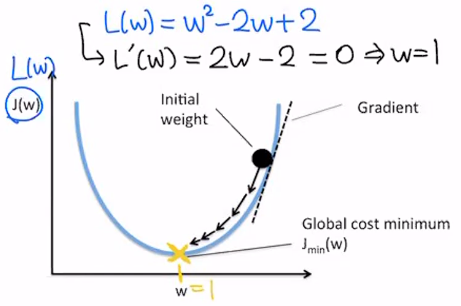
analytic solution을 찾기 힘든 이유

1. feature space가 일반적으로 다차원임
2. L(w)가 convex가 아님

3. 다차원 공간에서 미분한 결과(수학적으)로 최소를 찾기 힘듦.

   e.g. saddle point

• 골짜기 가장 밑바닥으로 내려갈 수 있는 현실적인 방법 → loss function의 최소가 되는 지점

  미분을 했을 때 0이 되는 지점 중 가장 작은 값

• 각 지점에서 기울기 (gradient)가 가장 큰(가파른) 방향으로 내려갑니다.

  가장 큰 방향 (gradient vector) → 미분해서 찾는다

• 한 번에 얼마나 내려가느냐(learning rate)에 따라 내려가는 속도가 결정됩니다.

  → hyper-parameter

  ### “Gradient Descent Algorithm”

  $w\prime \leftarrow w - \nabla w \cdot \alpha$

위 그림에서의 w

→ local optima : 극소 (무조건 최소를 찾는게 보장되지는 않음)

global optima : 최소

Loss Function이 convex인게 정해져있으면 무조건 global을 찾을 수 있음

Linear Regression의 경우 Loss function이 convex이기 때문에 잘 찾을 수 있음